Bar modelling in early maths - how is it beneficial?

Bar modelling is often credited as a central pillar in the successful mathematics curriculum and pedagogy of Singapore and other East Asian nations. Furthermore, the Mastery approach evolving in the UK has led to an increased focus on bar modelling and the CPA method.The TES has several excellent articles on this. More recently, New Zealand schools have shown a growing interest in this method as a tool for developing learner agency and accessing problem solving. But, when and how should be introduced?

Is there a place for bar modelling in early maths?

As children move towards the abstraction of using numerals, using the bar model can help children combine the ordinal and cardinal aspects of number. In the example below, the brace/bracket used in bar modelling labels the number of objects. This could be a technique adults might use and model to children during early counting experiences.

Teachers familiar with Martin Hughes' seminal work might suggest the example above is too big a conceptual leap for children without one-to-one correspondence. His work suggested that children used pictographic and iconic marks before the symbolic use of numerals. The examples below show how children might label amounts of objects pictographically or iconically before moving to using numerals.

An example of iconic labelling

An example of pictographic labelling

Developing 1-1 correspondence 

It could be argued that these images and experiences are not different to any early years classroom. Giving children rich experiences of counting, classification, sorting and identifying pattern are cornerstones of early mathematical experience. I'd argue that the bracket or brace encompassing the objects that are being counted is very powerful. I believe that this helps to cement the cardinal aspect of number, consolidating the 'threeness' of the objects.




Look at the image below, if we were to ask the question, 'where is the 3?' Would children point to the 3rd train on the right (assuming they have counted from left to right)? The brace helps us to show that once we have counted the third cube (whichever cube that may be) we know the number in the set.

The next step for young students is to begin bar modelling. Again, we encourage children to build on their counting experiences and manipulate concrete apparatus. Here the model is discrete, and still encourages and supports one-to-one matching. This also highlights the abstraction principle of counting. Children begin to see that they can count the pictorial representation of the block rather the block itself.

A discrete bar model

Developing counting strategies, calculation and understanding of pattern

The next step in the progression is to move from a model of 3 ones to a continuous model of one group of 3. Conceptually this is a significant change in understanding. I'd argue that it isn't sufficient to do this only by bar modelling. Educators need to consider whether they have grouped objects for students to explore. This is where Numicon and Cuisenaire are so powerful and, for me,  crucial maths resources for teaching.

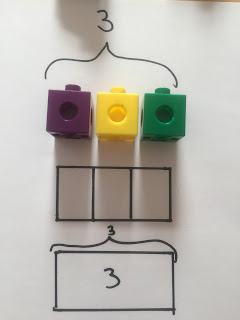Moving from a discrete model to a continuous model

Now that the 3 the in photograph above has been unitized we can work with it. So, we could place another 3 alongside it and begin thinking about multiplication as repeated addition. First though, we are developing counting strategies. In the calculation, '3+2'  a developmental step would be to count all of the objects (or blocks in the bar) but now the 3 is continuous children have a scaffold to help them count on from 3, rather than begin by counting the objects within the 3.

The bar model to count on

The above image is similar to a number line. My issue with a marked number line is that children can still count from 0 to get to 5. Furthermore, with the progression shown above, children who are just moving past the one-to-one correspondence stage may be able to picture the 3 other cubes within the continuous bar. This type of mental imagery is vital in helping children develop number.

The next step would be to draw two continuous bars labelled 3 and 2 next to each other. At this point, I'd ask educators to consider how they move children away from the developmental stage of counting to calculate. The question could be rephrased as, 'Which manipulatives are you using to secure knowledge of number facts?' Numicon, Cuisenaire, tens frames and bead strings, all offer children a variety of experiences with number. Personally, I feel that Numicon is the most powerful - I'll save that blog for another day.

Where next with Bar modelling?

Once children have experience developing their additive reasoning with concrete apparatus and bar models, they can then be used to develop (or assess) their multiplicative understanding. Starting to use bar modelling and its principles early on, will mean students are familiar with it and its conventions for different aspects of number.

Bar modelling for young children - how is it beneficial?

Hopefully, this has answered some of your questions regarding using the bar. My previous post discusses bar modelling as a problem solving tool for increasing learner agency. Nick Hart's blog is also an excellent resource.

How do I get this into my classroom?

At first, including bar modelling in your classroom can be quite daunting. As with any new pedagogy, it is important to understand the principles behind the method. Sign up to a training course!

UK educators, go here. The White Rose training is exceptional. NZ teachers, you can access the same training by attending a CPA Maths workshop

The power of bar modelling

I am delighted to have completed the Train the Trainer course from White Rose Maths Hub. It's incredibly exciting; I can now share this fantastic training. The blog is an attempt to show what a powerful tool it is.

Bar modelling does two things:

1) Provides a pictorial support for understanding mathematics
2) It gives a scaffold for children to access problem solving

This problem is often categorised as trial and improvement. We choose a number for day 1. Then work from there. Quickly realising that the number has to be less that eighty. Quite significantly less than 80 as day 1 and 2 are two numbers quite close together. Eventually, through trial and improvement we will find an answer. This a year 3 or 4 problem.

How does Bar Modelling support problem solving?

1) A starting point. The model helps me understand the structure of the problem identify knowns and unknowns.

2) What's changing? Day 2 has 4 fewer castles than day 1. While day 3 has 4 fewer castles than day 2 but also 2 lots of 4 fewer than day 1.  Day 4 will have 4 fewer than day 3 but 2 groups of 4 fewer than day 2 and 3 group of 4 fewer than day. Here, the image supports the more abstract explanation.

3) 5 bars of equal length! I can use my multiplicative reasoning. N divided by 5 gives the length of each bar.

4) I am making progress, but have I answered my question? The question marks in the model help students to check they have completed the question.

I believe that the power of bar modelling lies in helping highlight the structure of problems. It helps children to identify patterns and use what they already know. The incredible @mrnickhart has written some excellent articles on this and the inadequate use of RUCSAC. Now I realise how accessible, simple and empowering bar modelling is I cringe at memories of my former (non-bar modelling) self pointing at the RUCSAC display. As Dylan William says, "This job you’re doing is so hard that one lifetime isn’t enough to master it. So every single one of you needs to accept the commitment to carry on improving our practice until we retire or die. That is the deal.”

Nick Gibb: building a renaissance in mathematics teaching. But what about the foundations?

In 2016, Nick Gibb stated that:

In countries such as Korea and Singapore, and cities such as Hong Kong and Shanghai, the percentage of low-performing 15-year-olds is below 10%. There is nothing different about children in these countries, but there is something different about their approach to teaching maths.


Pisa results don't lie. The UK came 27th in 2015

There has been a real change in the teaching and learning of mathematics in the last 3 years; there is no doubt that Mr Gibb is having a huge influence in our classrooms. The new National Curriculum and the term mastery have caused schools to evaluate their processes and some long-standing facets of educational DNA have disappeared. My words. Nick Gibb's words below:

Today, I want to celebrate a renaissance in mathematics teaching that is taking place in our schools. Currently happening on a small scale, it has the potential to revolutionise the teaching of the subject in this country.

At this point, I'd like to address the term mastery. A term Nick Gibb uses quite liberally. Some schools and teachers use the term, I believe, without much substance. Is it a noun? Is it an adjective?

Is that a mastery lesson? Is that mastery? Can you give him some mastery questions? Is he at Mastery?

The NCETM discuss the different terms here. Even better, read @emathsuk excellent and accurate overview of mastery via Bloom and Washburne here. @mistersetchell rather elegantly navigated this problem at a course I attended by using the term, messages around mastery.

It's my belief that those messages around mastery have improved aspects of teaching:

• Reasoning 
• Problem solving 
• Not placing limits on learning through prison-like grouping 
• CPA 
• Teaching for understanding 
• Concrete-pictorial-abstract approach 
• A belief all children can succeed - although my previous post disputes this somewhat

So, our classrooms are changing, our practice is changing, both myself and the Secretary of State for schools notice the difference. Surely, we will catching up with the high performing jurisdictions that Mr Gibb eulogises about?


2016 KS1 Mathematics results

Look closely white British 73% at the expected levels and 17 percent at higher standard. Children of Indian origin 82% at and 29% higher. Finally, Chinese 88% at and 40% at higher standard.
Similar patterns can be found in the 2016 KS2 results:


92% Chinese at the expected level.

There is a stark difference in attainment between the different groups. We live in a culturally diverse country; there's no doubt this is a very reductionist approach to looking at the education of young people. However, when the Minister for schools is hailing education systems from around the world with such reverence, it would be remiss not to dig a little deeper.

In 2016, Nick Gibb stated that:

In countries such as Korea and Singapore, and cities such as Hong Kong and Shanghai, the percentage of low-performing 15-year-olds is below 10%. There is nothing different about children in these countries, but there is something different about their approach to teaching maths.

I conjecture there is something different. The data shows that students of Chinese origin perform incredibly well in our system. The difference is not just the approach to teaching maths, but in the approach to learning maths as well. Nick Gibb may be building a renaissance in mathematics teaching - but what about the foundations?

The birthday lottery

In a maternity ward somewhere, a Father-to-be paces the bare corridors, twiddling his thumbs. The ante-natal classes didn't prepare me for this he muses to himself. This birth is much more complicated than that of his previous children. It is late into the night of the 31st August and this primary mathematics teacher knows his statistics. Either side of midnight changes everything.....

So let's look how..

The 2016 pupil data for Key Stage 2 is in the table above.  The percentage of children reaching the expected standard born in September 75. In August only 65% made this standard.

Even a poorly made bar chart on excel can highlight the relationship (apologies for the shortened y-axis)

My next stop took me to the data for the KS1 assessments. To make a point this y-axis starts at 0.

The percentage of children reaching the expected standard drops from 82% (September birth) to 61% (August birth).  When we look at pupils known to be eligible for free school meals, 58% of these pupils made the expected standard. Of the other children, 75% of children made expected in maths. The September to August gap was 22% while the disadvantaged gap was 17%. Let's consider the profile and financial expenditure on disadvantaged children. Is there similar emphasis on summer born children? Most teachers don't know this effect exists.

I wanted to know whether the 'increased expectations' of the National Curriculum and the associated assessments were magnifying this issue.  I can't find any data of old SATS to compare against. I'd be grateful for anyone to share this if they have.

The eagled-eye of you will have spotted that this doesn't just apply to maths but the trends are evident against other curriculum subjects. I've focused this blog on mathematics because of the sea change this country is undergoing in terms of mathematics educations. The Shanghai visits and the shiny new textbooks are unlikely to reverse this trend. Furthermore, the evidence above disputes one of the definitions of mastery - the definition that everyone can learn maths to a high degree -because the data clearly states that birth month will affect your chances of making the standard. We could argue the that arbitrarily high expectations of the curriculum puts a moving developmental ceiling on some learners who have had less time to develop. It is difficult to argue this without evidence from the previous assessment regime. Perhaps, we need a scaled score dependant upon DOB. Something much more akin to standardised tests

What I do know is, in 3 weeks time some children will leave primary school labelled as failures. That itself is heartbreaking. The likelihood of that is much higher if you they are summer born. No-one is talking about that....yet.